Bruce Lee once said, "I fear not the man who has practiced 10,000 kicks once, but I fear the man who has practiced one kick 10,000 times." This timeless wisdom applies to almost any field of study, including poker. Much like martial arts, poker is a game that requires a deep understanding of strategy, patience, and discipline. When it comes to playing poker well, it's essential to focus on perfecting the fundamentals. Fancy and flashy plays constantly happen at high-stakes cash games and tournaments, so naturally, many less experienced poker players think, "I need to play like this to win".

To get to the point where you will be able to understand and make these crazy moves, you need to develop a solid foundation from which to build your poker strategy. Then, once you know how the game works, you can start getting more creative. In this article, we'll review the core principles and concepts that poker is built upon.

A few basics concepts to play poker correctly

Like a martial artist learning to throw a jab, a poker player must start by understanding the basics of the game before diving into the depths of game theory optimal.

At its essence, poker is a game of winning the blinds (and antes). The blinds are forced bets that players (usually two) make before the hands are dealt. These forced bets are necessary to incentivise other players to put more money into the pot. Without the big and small blind, there would be nothing to gain, so why would anyone risk their money without pocket aces? The blinds create a starting pot, a poker game dynamic that allows for the concepts of odds and equity to arise. Due to their existence, we can now use probability and math to make decisions.
So before you jump into solvers, let's look at some fundamental poker concepts.

Poker equity and hand strength

Equity is the probability that your hand wins by the river on average.

If you were dealt AA whilst your opponent was dealt a random hand and we would run out the all the possible board combinations, we would find that AA wins about 85% of the time.

Of course, equity can change during the hand. You also have to measure equity in relation to other hands that are possible in a given situation.

This is where the concept of hand strength arises.

Hand strength is both absolute and relative. What does this mean? You should always evaluate your hand strength in relation to the board texture and what your opponent is likely to have. Having pocket Aces is a great starting point, but if the board is 98654 with four hearts and you aren't holding a heart, then your Aces are likely no good. This example is extreme, of course, but you get the point. Hand strength changes throughout the poker hand quite often on every subsequent street. You may start with a strong hand like Aces, but the board can run out in a way that makes it very unlikely that you will win.

Expected Value

If you've ever played poker, you've probably heard the term "+EV" thrown around.

To be a solid poker player, you need to understand the importance of expected value and how it is calculated.

EV = (chance of winning × amount we expect to win) - (chance of losing × amount we expect to lose)

Assuming probability of win + lose = 100%.

EV allows you to estimate whether a play we consider is profitable or losing. Being able to estimate the average outcome allows you to determine whether or not you should make a given play.

As the GTO poker dictates, to make the most money in poker is to find the highest EV play at any decision point in a hand.

A cash game example

You get to a river with a bluff, and you want to figure out if betting to get a fold will be profitable. Let's make some assumptions.

Let's say the pot is $100, and you bet $100

You think your opponent is going to fold 50% of the time.

What's the expected value? Using the formula that we introduced above, you can calculate the EV of your play.

Chance of winning = 50% (opponent folds 50% of times)
Chance of losing = 50% (opponent continue 50% of times)

The amount we expect to win = $100
The amount we expect to lose (our bet) = $100

EV = 0.5 × 100 - 0.5 × 100
EV = 50 - 50
EV = 0

Answer: Our EV is $0. This bluff is exactly break-even.

Poker pot odds

This is the ratio between the current size of the pot and the cost of a call or bet. Understanding your equity and applying it to pot odds is how you estimate a play's EV (Expected Value).

So, whenever you consider calling, compare the pot odds with the odds of you winning the hand at showdown.

This is the "break-even percentage" or, in other words, a threshold of how often you need to win for a hand to be a profitable call.

Break-even percentage = amount to call / (pot + opponent's bet + amount to call)

So, let's assume our opponent bets $50 into a pot of $100

Break-even percentage = ($100 pot + $50 Opponent's Bet + $50 Call amount)

Break-even percentage = $50/$200

Break-even percentage = 0.25 or 25%

Why is this important to understand?

We make money if our opponent bluffs more often than the break-even percentage.

In contrast, if our opponent undershoots this frequency, a call will become losing.

So much of our analysis when deciding whether to call or fold is based on calculating our pot odds and estimating our opponent's bluff frequency.

This can also be applied when making a bluff:

First, we calculate our break-even percentage on a bluff

Let's assume the pot is $100 and we bet $50

Break-even percentage = bluff bet amount / (pot + bluff bet amount)

Using the example above:

Break-even percentage = $50 / ($100 + $50)

Break-even percentage = $50 / $150

Break-even percentage = 0.3333 or 33.33%

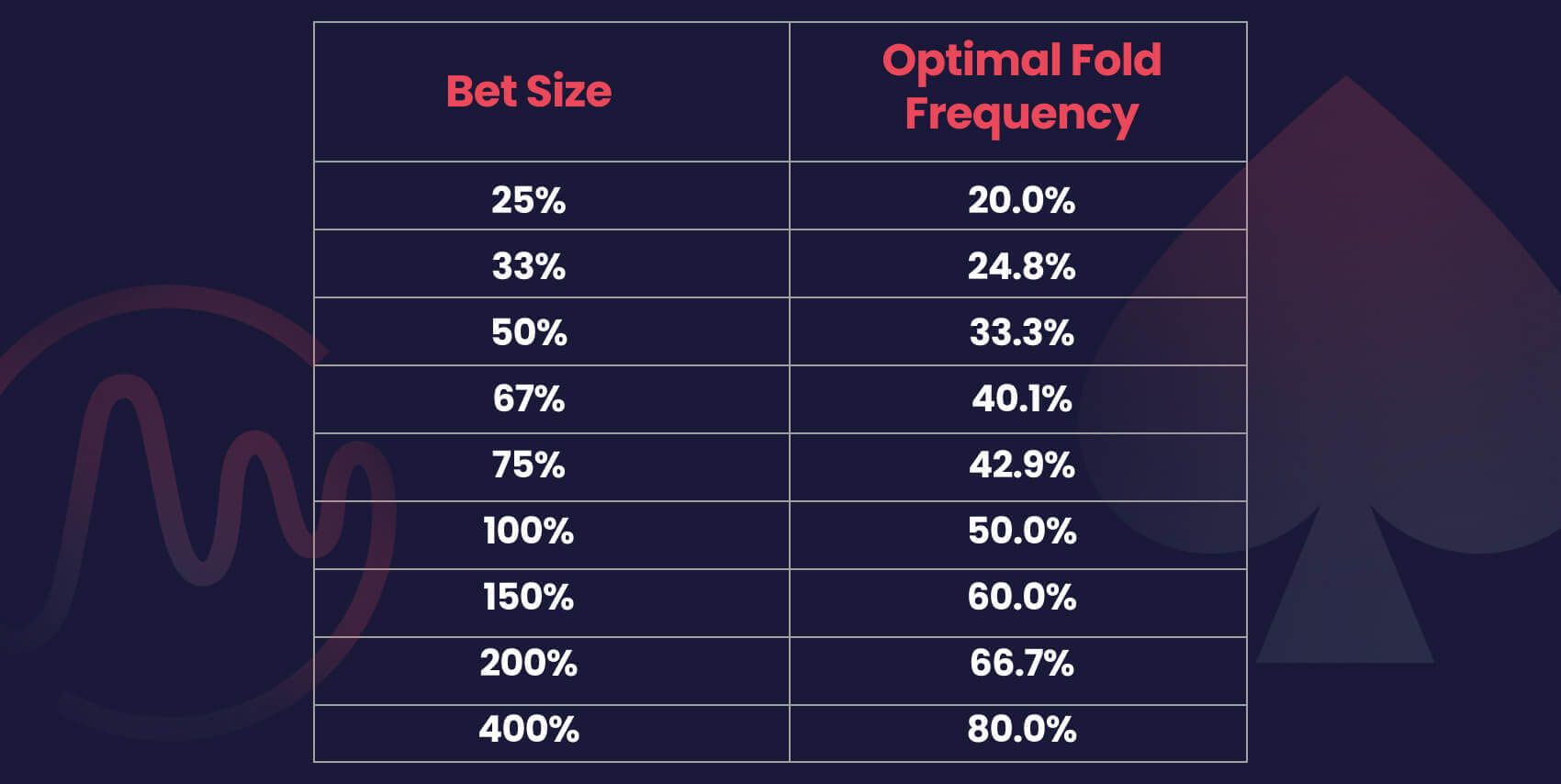
Note that many poker resources will refer to an optimal "defense" frequency which is simply (1 - optimal fold frequency) or 1-α.

Indifference in a poker game

You might have noticed we've titled the above tables "optimal bluff frequency" and "optimal fold frequency".

It refers to a concept known as indifference. Indifference occurs when you don't prefer one action over another. This situation arises when the expected value of both actions being equal.

If a player folds at exactly the optimal fold frequency based on the size we've bet, then we would have no preference as to whether or not we bluff since bluffing is no better than checking. If a player bluffs at exactly the optimal bluff frequency, we have no preference between calling or folding when holding a bluff catcher.

In reality, we will very rarely be indifferent. The reason is simple; humans often play very far from the GTO poker principles. So, in many cases, you should prefer one option over another.

However, understanding the indifference points in these cases allows you to gain insight into how to build a poker strategy. If you know roughly what frequency to bluff and call in a given situation, you can use this to estimate our expected value using assumptions.

It also gives you an exploitative mental framework to make bluff or call decisions.

Bluff-catching example:
Our opponent bets pot; we think he's bluffing about 40% of the time. Should we call?

If we reference the above table, we can see that the optimal bluff frequency for a bet size of pot is 33.33%.

Since 40% > 33.33%, we can assume that calling will be profitable since their bluff frequency is higher than optimal.

Bluff example:
If I bet 200% pot, I think my opponent will fold about 80% of their hands.

Using the table for reference…

Optimal fold frequency vs 200% pot = 66.7%. 80% fold > 66.7% fold frequency

The beautiful part about these concepts is that whilst we haven't touched a solver or looked at a sim so far, they pop up all over the place when we look at solver outputs. Of course, you could jump in and start looking at solutions without understanding these ideas, but these ideas give you context. They allow you to see when to deviate from the solver.

You don't need a solver to understand the basics of a GTO poker strategy

In summary, the theoretical underpinnings of poker are based on math. Understanding how to estimate EV based on the equity and pot odds in a situation will allow us to evaluate the profitability of a situation.

Exploits can be found when our opponents break the indifference principle, leading us to prefer always bluffing, calling or folding.

Want to learn more about poker concepts? Join our growing Discord community!